免费上门看货,诚信定价,当场结算

品质保证
13315260828
免费上门看货,诚信定价,当场结算

废变压器回收公司,专业回收变压器公司,变压器回收厂家双墨回收全国上门回收,资金雄厚,量大价高,快速结款,欢迎咨询!
变压器回收之变压器的轻微匝间短路故障实例及分析
1997年5月6日开封滨河变一台110 kV/10 kV,31 500 kV*A变压器发生事故,变压器差动保护正确动作跳闸,瓦斯保护未动作。
事故后对变压器进行各种外部试验都未能发现故障。内部检查为高压侧A相匝间短路,被短路的匝数约占全部绕组的1%。这次事故是典型的轻微匝间故障,对此有深入分析研究的必要。
图1是该事故的故障录波图,其显示高压侧三相电压和低压侧电流都没有明显的变化。打印报告显示故障前高压侧负荷电流二次值为2.04 A,CT变比为300/5,所以约为0.74In。故障后三相电流的基波值分别为IA=5.27 A,IB=2.27 A和IC=3.83 A,变压器高压侧中性点未接地,故3I0=0。
全国上门回收变压器,量大价高,可按台或按吨回收
回收热线:13521663353
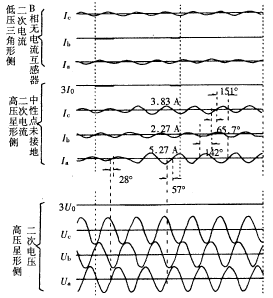
图1 开封滨河变1997年5月6日
高压A相匝间短路录波图
事故前功率因数较高,假设cos?φ=0.9,从录波图上量出?φ=28°,说明假设合理。由于高压侧中性点未接地,A相匝间短路引起的故障分量电流ΔIA只能由B,C相流回,因此有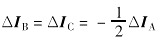 。假设ΔIA落后UA 80°,可作出三相电流的相量图(如图2)。从图2可得IA=ILA+ΔIA=5.27∠-60°A;IB=ILB+ΔIB=2.27∠-198°A;IC=ILC+ΔIC=3.83∠-263°A。此结果与打印报告中电流的幅值和从录波图上量出的相角十分接近,故假设IA落后UA 80°是正确的①。从图2可测量出ΔIA=4∠-80°A,约等于变压器的额定电流1.45In。 电流的故障分量即继电器的差动电流, 但为了校正Y/Δ变压器两侧电流相位, 差动继电器测量的差动电流应是高压侧两相故障分量电流之差, ΔIAB=ΔIA-ΔIB=2.17In∠-80°, ΔIBC=0, ΔICA=-2.17In∠-80°。两相电流差的额定值为
。假设ΔIA落后UA 80°,可作出三相电流的相量图(如图2)。从图2可得IA=ILA+ΔIA=5.27∠-60°A;IB=ILB+ΔIB=2.27∠-198°A;IC=ILC+ΔIC=3.83∠-263°A。此结果与打印报告中电流的幅值和从录波图上量出的相角十分接近,故假设IA落后UA 80°是正确的①。从图2可测量出ΔIA=4∠-80°A,约等于变压器的额定电流1.45In。 电流的故障分量即继电器的差动电流, 但为了校正Y/Δ变压器两侧电流相位, 差动继电器测量的差动电流应是高压侧两相故障分量电流之差, ΔIAB=ΔIA-ΔIB=2.17In∠-80°, ΔIBC=0, ΔICA=-2.17In∠-80°。两相电流差的额定值为 In,所以此时差动继电器测得的差动电流相当于额定值的
In,所以此时差动继电器测得的差动电流相当于额定值的 125%。事故时变压器差动继电器的启动电流的整定值为0.5In,因而能灵敏地动作。
125%。事故时变压器差动继电器的启动电流的整定值为0.5In,因而能灵敏地动作。
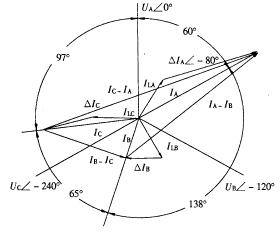
图2 根据录波图作出的三相电流的相量图
变压器回收,这次事故至少引发出以下三个问题,值得我们思考。
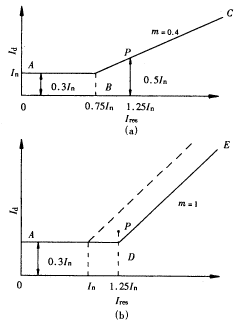
(1) 差动保护能够保护轻微匝间故障。长期以来在我国广泛应用由速饱和变流器供电的机械型差动继电器。其有两大缺点:最小启动电流必需大于1.5In才能保证避开励磁涌流,因而对轻微匝间短路不灵敏;当短路电流中有直流分量时动作速度变慢,越是加强速饱和变流器的作用带来的延时越长。若故障靠它切除变压器烧损得十分严重。若有很好的涌流闭锁元件,差动继电器就可以灵敏地、快速地动作,把变压器故障烧损的程度限制到最小,开封滨河变的事故已证明了这种可能性。
(2) 轻微匝间短路时保护能测量到的最小差动电流有多大?轻微匝间短路时测量到的差动电流肯定比在变压器低压侧引线上短路时小得多。错误地用后者作为校验差动保护灵敏度的标准也是造成差动保护不能在匝间故障时起保护作用的原因之一。开封滨河变事故时的故障电流水平有无普遍意义?轻微匝间短路时的最小差动电流如何确定?这些问题需研究解决。
(3) 如何选择制动特性。轻微匝间短路时,一方面故障电流小保护的差动电流就小;另一方面三相电压正常,可继续送出满负荷电流。负荷电流是穿越性的,将产生制动作用,于是很自然要问在此制动作用下,继电器能否动作?我们应当选择什么样的制动特性?
变压器回收公司,以下对差动继电器能否在轻微匝间短路时起保护作用的问题进行进一步分析。
2 变压器匝间故障的计算
变压器绕组的故障都属于匝间短路故障。以Y/△接线的双绕组变压器在高压星形绕组发生匝间短路为例,把短路绕组和高压绕组分离开来(健全相相应的部分也如此),于是故障后的变压器变为一个Y/Y/△接线的三绕组变压器(当然高压绕组的匝数减少了),故障发生在短路绕组一侧的引线上。由此可见匝间短路有多相与单相之分。最常见的尤其是轻微匝间短路都是单相的。为了节省篇幅仅讨论单相匝间短路。
图3示出计算用系统图及在变压器高压绕组发生单相匝间短路的复合序网图,变压器被看成是三绕组变压器,其等值回路是由三个漏抗ZH,ZL,ZK按星形连接的回路。H,L,K分别表示高压侧、低压侧及短路绕组侧。Z1LD和Z2LD为低压侧的正、负序负荷阻抗。高压侧中性点接地时刀闸S闭合,否则S断开。计算的困难在于确定变压器等值回路中的三个漏抗ZH,ZL,和ZK。
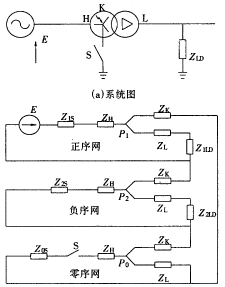
图3 单相匝间短路计算用
系统图及复合序网图
变压器绕组的漏抗决定于漏磁通所经路径的磁阻,而漏磁通的路径十分复杂(以下的计算参考文献[2])。但是在故障前的漏抗是已知的,只要分析出短路后各绕组与原绕组的关系就可近似地得到故障后形成的三绕组变压器的各侧漏抗。
众所周知,对于三绕组变压器通过试验或计算只能依次求得两个绕组之间漏抗,如ZHK,ZHL和ZLK。把它们归算到同一侧如高压侧,那么图3中星形等值回路中的各阻抗为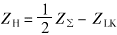
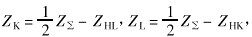
式中 ZΣ=ZHK+ZHL+ZLK。
从滨河变故障录波分析知道ΔIA落后UA 80°,说明漏抗中有效电阻的成分很小,以下计算中都忽略电阻以漏电抗代替漏阻抗。
为了简单,假设绕组是圆筒形的。圆筒形绕组的漏磁通的路径有效长度决定于绕组的高h和有效厚度d。通常在计算时把厚度折合为高度得到磁路的有效高度或有效长度h′=kh,其中k是折合系数,一般k=1.1。显然k与比值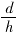 有关。短路绕组的高度等随着短路匝数而变化,其折合系数也要随之变化。为了简化,下面取实际高度ht与有效厚度d=0.1ht之和作为磁路的有效长度h′,ht为原来整个绕组的实际高度。于是如果短路绕组匝数占原高压绕组总匝数之比为α(1>α>0),则短路绕组的实际高度为αht。短路绕组的漏磁通的路径的有效长度与原有效长度之比为
有关。短路绕组的高度等随着短路匝数而变化,其折合系数也要随之变化。为了简化,下面取实际高度ht与有效厚度d=0.1ht之和作为磁路的有效长度h′,ht为原来整个绕组的实际高度。于是如果短路绕组匝数占原高压绕组总匝数之比为α(1>α>0),则短路绕组的实际高度为αht。短路绕组的漏磁通的路径的有效长度与原有效长度之比为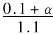 。设变压器原有的漏抗为Xσ。以下依次计算三对绕组之间的漏抗。
。设变压器原有的漏抗为Xσ。以下依次计算三对绕组之间的漏抗。
(1) 高压绕组和短路绕组之间的漏抗X?HK。绕组的漏抗与匝数的平方成正比,与磁路的有效长度成反比。高压绕组去除短路绕组后的匝数,与短路绕组匝数占原来总匝数之比分别为1-α和α。这两部分圆筒的半径相同,是叠起来的,它们之间的漏磁通不穿过铁芯,全部在空气中形成环路,有效高度要加大一倍。短路绕组漏抗将是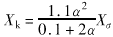 ,其归算到高压侧之值为
,其归算到高压侧之值为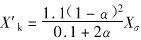 。同理高压绕组的漏抗为
。同理高压绕组的漏抗为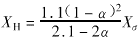 。于是可得
。于是可得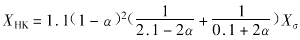 。
。
(2) 高低压绕组之间的漏抗XHL。绕组的漏抗与漏磁通路径的截面成正比。在绕组直径一定时截面与绕组等效厚度(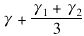 )成正比。γ为两绕组之间气隙的宽,γ1和γ2分别为两绕组的厚度,漏磁通的一部分仅与高压绕组相连,另一部分仅与低压绕组相连,它们分别决定每一绕组的漏抗。要求每一绕组的漏抗,必须确定这两部分漏磁通在空间的分界线,这是困难的。试验也无法确定每一绕组的漏抗。计算时一般认为两绕组的漏抗(归算到同一侧的值)是相等的。
)成正比。γ为两绕组之间气隙的宽,γ1和γ2分别为两绕组的厚度,漏磁通的一部分仅与高压绕组相连,另一部分仅与低压绕组相连,它们分别决定每一绕组的漏抗。要求每一绕组的漏抗,必须确定这两部分漏磁通在空间的分界线,这是困难的。试验也无法确定每一绕组的漏抗。计算时一般认为两绕组的漏抗(归算到同一侧的值)是相等的。
已知的Xσ是原来两个绕组漏抗的和,与Xσ相对应的漏磁通占据了整个截面。在上面计算XHK时因为每一绕组的漏磁通都占据了整个截面就直接以Xσ为基准进行计算。现在计算XHL就必须注意到漏磁通路径截面在两个绕组间的分配。
变压器回收,现高压绕组的匝数和高度都减少了,整个绕组都面对着低压绕组,它的漏磁通路径的截面应减少一半,计算时所用的基准电抗也应减少一半。所以高压绕组的漏抗为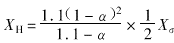 。低压绕组完好如初,匝数和高度都没有变化,但一部分(1-α)WL面对高压绕组,其余αWL则否。前一部分产生的漏磁通的路径的截面应减少一半,后一部分则否。因此低压绕组的漏抗(归算到高压侧的值)应为
。低压绕组完好如初,匝数和高度都没有变化,但一部分(1-α)WL面对高压绕组,其余αWL则否。前一部分产生的漏磁通的路径的截面应减少一半,后一部分则否。因此低压绕组的漏抗(归算到高压侧的值)应为 。于是可得
。于是可得
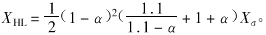
(3) 低压绕组与短路绕组之间的漏抗XLK(归算到高压侧的值)。短路绕组都面对低压绕组,所以计算的基准电抗要减少一半。其归算到高压侧的值为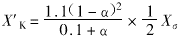 。低压绕组的一部分αWL面对短路绕组,其余部分则否。它归算到高压侧的值为
。低压绕组的一部分αWL面对短路绕组,其余部分则否。它归算到高压侧的值为 ,所以低压绕组与短路绕组之间的漏抗(归算到高压侧的值)为
,所以低压绕组与短路绕组之间的漏抗(归算到高压侧的值)为
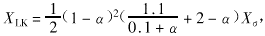
求出XHK,XHL,XLK后就可求出图3中等值回路中的XH,XL,XL。
表1示出对于几个不同α值计算得到的漏抗(相对于Xσ)之值。
表1 变压器匝间短路不同α值下的等值回路参数
| α | 0.01 | 0.025 | 0.05 | 0.1 | 0.2 | 0.5 |
 |
2.17 | 1.67 | 1.11 | 0.67 | 0.42 | 0.25 |
 |
-1.18 | -0.69 | -0.16 | -0.22 | 0.35 | 0.17 |
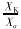 |
7.05 | 5.81 | 4.35 | 2.77 | 1.4 | 0.25 |
| Xσ | 0.08 | 0.11 | 0.14 | |
| Id* | α=0.01 | 0.78 | 0.56 | 0.45 |
| α=0.025 | 0.96 | 0.70 | 0.55 |
| m=kres | 0.20 | 0.30 | 0.40 | 0.50 | 0.66 |
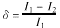 |
0.18 | 0.26 | 0.33 | 0.40 | 0.50 |
| I1/In | 1.5 | 2 | 3 | 4 | 5 | 10 | 15 | 20 |
| δ | 0.244 | 0.350 | 0.455 | 0.508 | 0.540 | 0.603 | 0.624 | 0.635 |